Manacher 算法

马拉车算法 (Manacher’s Algorithm) 主要用于处理字符串中的回文串，它可以在的O(n)时间里计算出以每个字符为中心的最长回文字符串。

回文，英文palindrome，指一个顺着读和反过来读都一样的字符串，如”abba”、“abccba”、12321、123321都是回文，而“abcde”和“ababab”则不是回文。

中心扩展

要获取字符串中的最长回文字符串，我们可以使用中心扩展法，即遍历字符串中的每一个字符，并以该字符为中心，同时向左右两边扩展，通过判断左右两边字符是否相同，获取到以该字符为中心的最长回文字符串：

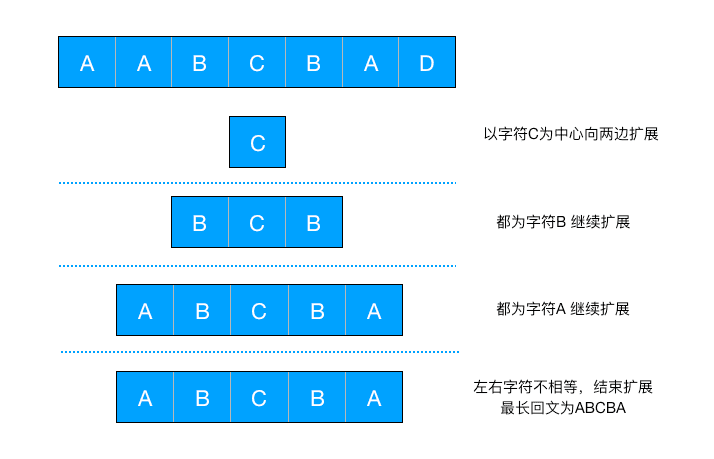
但是，如果回文字符串长度为偶数的情况下，就需要以当前字符和相邻右侧的字符整体为中心进行扩展：

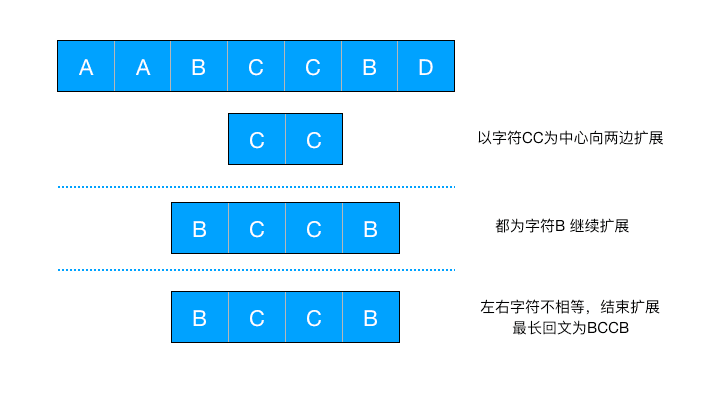
实现(java)

// 该方法的时间复杂度为 O(n²)
private static int getPalindromeMaxLen(String str) {
  if (str == null || str.isEmpty()) {
    return 0;
  }

  int start = 0, end = 1; // 默认回文长度1 end-start

  for (int i = 0; i < str.length(); i++) {
    int s = cal(str, i, i); // 奇数长度回文 aba
    int d = cal(str, i, i + 1); // 偶数长度回文 abba

    int r = Math.max(s, d);

    if (r > end - start) {
      start = i - (r - 1) / 2;
      end = start + r;
    }
  }
  // 输出最长回文长度 和 最长回文字符串
  System.out.println("len: " + (end - start) + ". str: " + str.substring(start, end));
  return end - start;
}

private static int cal(String s, int centerLeft, int centerRight) {
  int left = centerLeft;
  int right = centerRight;
  while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
    left--;
    right++;
  }
  return (right - 1) - (left + 1) + 1;
}

解决回文长度奇偶问题

可以看到中心扩展最大的问题，是对每一个字符都要按照奇偶分别处理，因此Manacher算法的第一步处理，就是在字符串每个字符中间插入特殊分隔字符 (如#)：

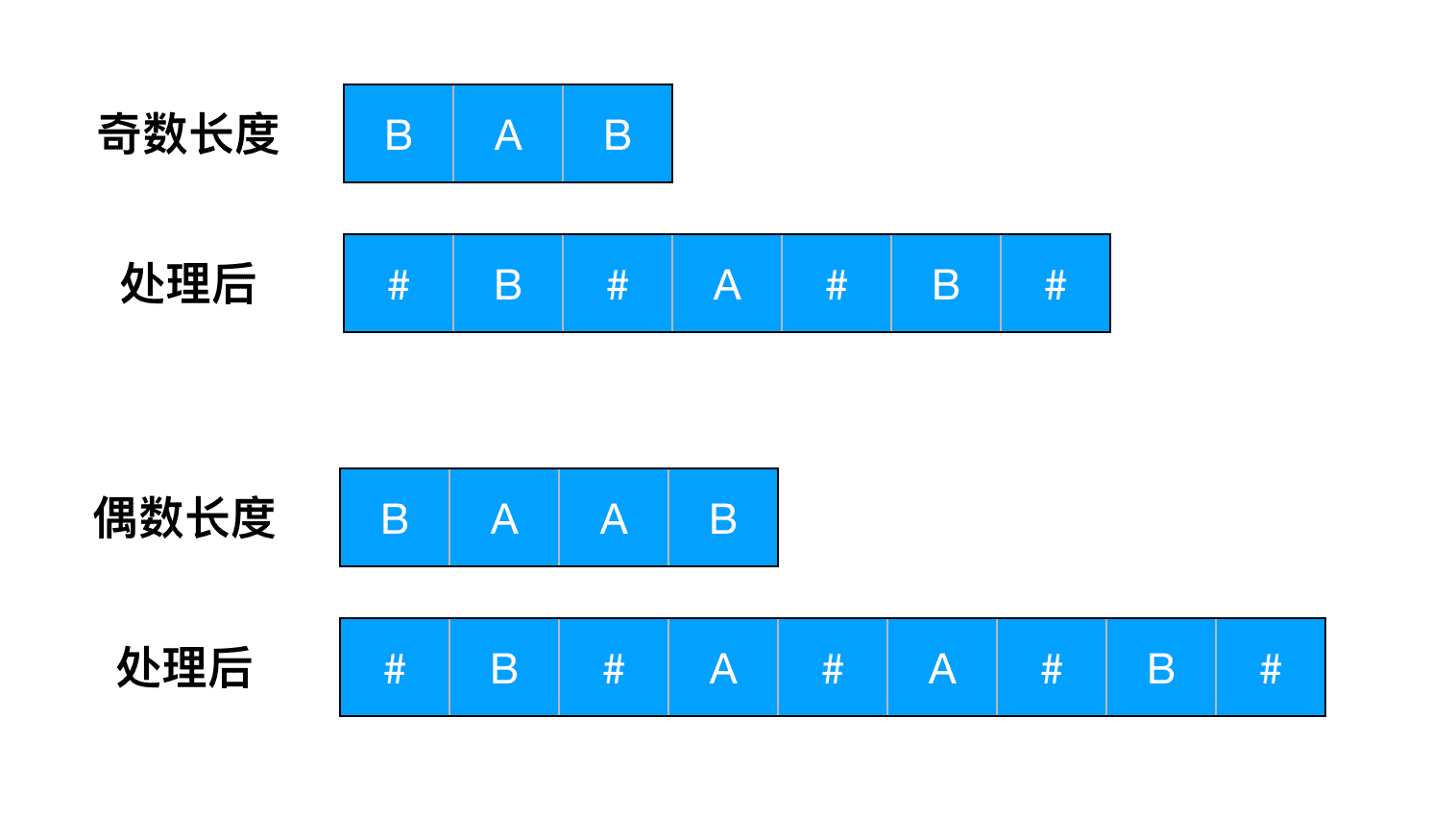
可以看到处理后的回文字符串，都变成了奇数长度，在这种情况下，如果把特殊字符也看做是字符串的一部分，那么中心扩展只需要计算奇数长度的回文即可。

计算最长回文

对处理后的字符串前后添加不同标识符 (如 ^ 和 $)，这样可以不用考虑到达边界的问题 (因为边界字符和分隔字符不同)，以字符CBCBCBB为例：

同时可以看到，P[i]其实就是对应原字符串中以每个字符为中心的最大回文长度，以T[10]=C为例，可以看到P[10]=3 (对应回文 #B#C#B#)，正好对应原字符串中最大回文长度 (BCB)。

对于如何计算P[i]，可以从左到右遍历所有字符，使用中心扩展法。但也可以从回文的特性出发，因为如果字符串是回文，那么必然是以中心字符C，R为半径，左右对称的字符串，在这种情况下，如果C左侧字符我们已经计算过回文长度半径，那是否可以直接将这个值直接映射到C右侧对应字符？如果这样，那么可以减少使用很多次的中心扩展法。

假设我们现在已经通过中心扩展法计算出了P[8]=6，那么我们可以以当前 i=8 为中心，计算出右半径位置RP:i=14以及左半径对应位置 LP:i=2 ：

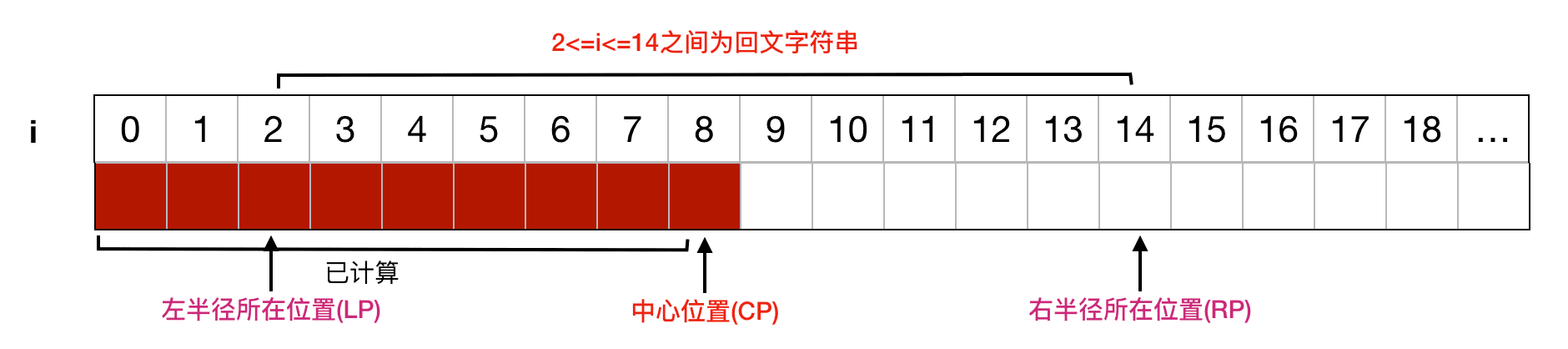
接下去我们要计算的就是 i>8 的情况，可以知道 i 必然是在 CP 右侧：

i在CP和RP之间

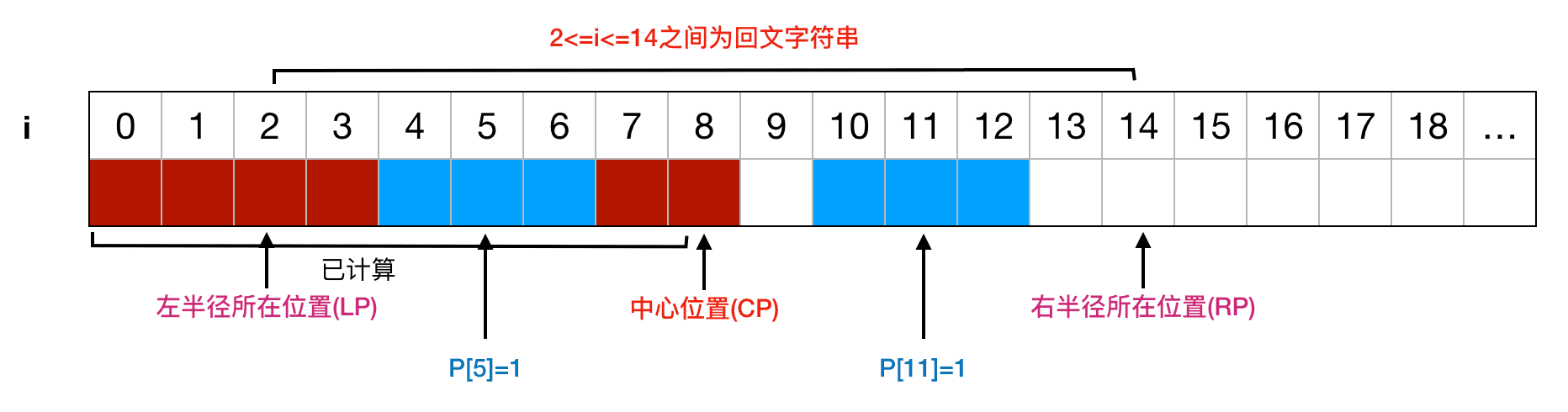
以 i=11 为例，可以计算出对应的映射位置为 i=5。

如果 P[5]=1，那么我们可以直接得出 P[11]=1 ：

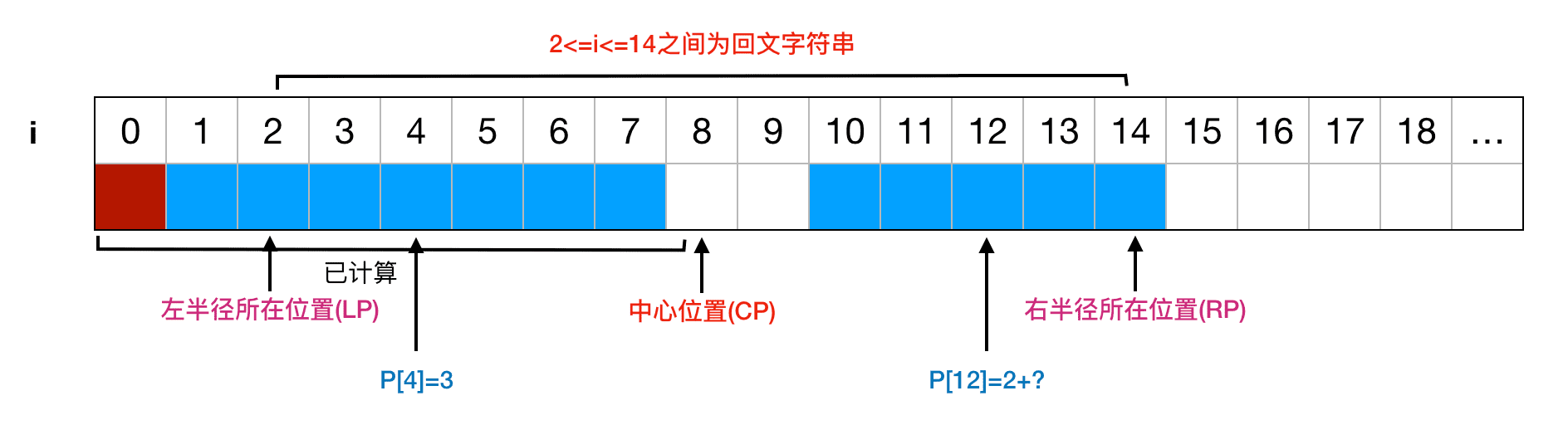
如果 P[4]=3，那不能直接认为 P[12]=3，因为P[4]的回文半径位置不在[LP, CP]之间，所以无法直接判定 T[9]=T[15]，或者换种思考方法，如果 P[12]=3，则 T[9]=T[15]，而 T[9]=T[7]，也就是 T[1]=T[15]，那么 P[8]=7，和条件中 P[8]=6冲突。因此在这种情况下，我们只能首先判定为 P[12]=2 (在R半径内是回文)，然后在此基础上继续向左右扩展：

总结来说，当 i 在 RP 左侧时，我们只能首先获取到 P[i] 的初始值 ( P[i]=min(RP-i, P[CP-(i-CP)])，然后在此基础上继续向左右扩展，直到比较到不同的字符。

i在RP右侧

这种情况下，说明 i 已经不在 CP为中心的回文内了，只能使用中心扩展法计算。

更新C和R

如果我们要使用镜像映射计算P[i]，那就需要尽量保证 i在 RP左侧，因而一旦 P[i] + i > RP时，我们就需要更新 C(CP) 和 R(RP)。

实现(java)

private static int getPalindromeMaxLen(String str) {
    if (str == null || str.isEmpty()) {
        return 0;
    }
    StringBuilder sb = new StringBuilder("^#");
    for (char c : str.toCharArray()) {
        sb.append(c).append("#");
    }
    sb.append("$");
    String T = sb.toString();

    int[] P = new int[T.length()];
    int CP = 0, RP = 0;

    for (int i = 1; i < T.length() - 1; i++) {
        int LP = 2 * CP - i;
        if (RP > i) {
            P[i] = Math.min(RP - i, P[LP]); // 2.1 情况，获取P[i]初始值
        } else {
            P[i] = 0;
        }

        // 中心扩展
        while (T.charAt(i + 1 + P[i]) == T.charAt(i - 1 - P[i])) {
            P[i]++;
        }

        // 判断是否需要更新 CP&RP
        if (i + P[i] > RP) {
            CP = i;
            RP = i + P[i];
        }
    }

    // 找出 P 的最大值
    int maxLen = 0;
    int centerIndex = 0;
    for (int i = 1; i < P.length - 1; i++) {
        if (P[i] > maxLen) {
            maxLen = P[i];
            centerIndex = i;
        }
    }
    int start = (centerIndex - maxLen) / 2; // 最开始讲的求原字符串下标

    System.out.println("len: " + maxLen + ". str: " + str.substring(start, start + maxLen));
    return maxLen;
}

时间复杂度：尽管代码里面有两层循环，但内层的循环只对尚未匹配的部分进行，对于每一个字符最多遍历 2 次，因此时间复杂度是O(n)。

参考

最长回文子串——Manacher 算法

Manacher Algorithm讲解

A simple linear time algorithm for finding longest palindrome sub-string