HashMap实现备注

发表于 分类于 本文字数： 2k 阅读时长 ≈ 7 分钟

image

本文仅对HashMap(1.8)源码中的部分实现细节做一个记录，不涉及到具体源码解析。

概念

首先明确几个概念：

  • bucket：假设数组的长度为16，那么我们可以认为有16个bucket
  • bins：bucket内的元素集合，每一个bin即链表(树)中的一个节点(代码实现中为node或者treeNode)
  • capacity：容量，即bucket的数量(数组的长度)
  • size：大小，即所有bucket中bin的总和
  • loadFactor：装载因子
  • threshload：扩容阈值，计算方式为capacity * loadFactor，当size > threshload 会进行扩容
  • treeify：树化，即将链表转为树
  • untreeify：去树化，即将树转为链表

HashMap类部分注释

首先看下HashMap类注释，其中简单介绍了HashMap的实现方式，在何时会进行扩容，扩容后会做何处理，以及为何装载因子要使用0.75：

……

// HashMap的初始容量和负载因子会影响HashMap的性能表现。当大小超过了(总容量*负载因子)时，HashMap会进行扩容，同时将内部元素rehash一次(也就是可能每个元素都会重新构建一次)
An instance of HashMap has two parameters that affect its performance: initial capacity and load factor. The capacity is the number of buckets in the hash table, and the initial capacity is simply the capacity at the time the hash table is created. The load factor is a measure of how full the hash table is allowed to get before its capacity is automatically increased. When the number of entries in the hash table exceeds the product of the load factor and the current capacity, the hash table is rehashed (that is, internal data structures are rebuilt) so that the hash table has approximately twice the number of buckets.

// 关于负载因子使用0.75，是因为这个数可以在时间和空间成本上有一个比较好的平衡。如果值太大，会减少空间成本，但是会增加查找成本。因此设置初始容量时，应该考虑预计大小和负载因子，以减少rehash的次数
As a general rule, the default load factor (.75) offers a good tradeoff between time and space costs. Higher values decrease the space overhead but increase the lookup cost (reflected in most of the operations of the HashMap class, including get and put). The expected number of entries in the map and its load factor should be taken into account when setting its initial capacity, so as to minimize the number of rehash operations. If the initial capacity is greater than the maximum number of entries divided by the load factor, no rehash operations will ever occur.

// 如果HashMap中需要存储很多元素，那么设置足够大的容量会比使用自动扩容的效果好。如果key的hashCode相同的情况下会影响性能，为减少这种情况的影响，HashMap将会使用key的比较关系来优化（此处即转为树结构）
If many mappings are to be stored in a HashMap instance, creating it with a sufficiently large capacity will allow the mappings to be stored more efficiently than letting it perform automatic rehashing as needed to grow the table. Note that using many keys with the same hashCode() is a sure way to slow down performance of any hash table. To ameliorate impact, when keys are Comparable, this class may use comparison order among keys to help break ties.

……

其中还有一段实现备注，记录了为何HashMap选择8作为链表转树的阈值：

Implementation notes.
……
// 前面部分说明了在链表长度大于阈值的情况下结构调整成树结构，下面这段说明了为什么选择8作为阈值。

// 树结构存储占用空间是链表存储的两倍，理想情况下，随机HashCode的后节点的分布遵循泊松分布，默认调整大小阈值为0.75，平均参数约为0.5，预期同HashCode节点长度出现的次数如下，当超过8时，概率已经小于千万分之一
Because TreeNodes are about twice the size of regular nodes, we use them only when bins contain enough nodes to warrant use (see TREEIFY_THRESHOLD). And when they become too small (due to removal or resizing) they are converted back to plain bins. In usages with well-distributed user hashCodes, tree bins are rarely used. Ideally, under random hashCodes, the frequency of nodes in bins follows a Poisson distribution (http://en.wikipedia.org/wiki/Poisson_distribution) with a parameter of about 0.5 on average for the default resizing threshold of 0.75, although with a large variance because of resizing granularity. Ignoring variance, the expected occurrences of list size k are (exp(-0.5) * pow(0.5, k) / factorial(k)). The first values are:

  • 0: 0.60653066
  • 1: 0.30326533
  • 2: 0.07581633
  • 3: 0.01263606
  • 4: 0.00157952
  • 5: 0.00015795
  • 6: 0.00001316
  • 7: 0.00000094
  • 8: 0.00000006
  • more: less than 1 in ten million

常量定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * 默认初始容量，必须2次幂
 */
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

/**
 * 最大容量，必须2次幂，并且要小于 1<<30
 */
static final int MAXIMUM_CAPACITY = 1 << 30;

/**
 * 默认装载因子
 */
static final float DEFAULT_LOAD_FACTOR = 0.75f;

/**
 * 将链表结构转为树结构的阈值
 */
static final int TREEIFY_THRESHOLD = 8;

/**
 * 将树结构转为链表结构的阈值
 */
static final int UNTREEIFY_THRESHOLD = 6;

/**
 * 当容量达到64时，转为树结构
 */
static final int MIN_TREEIFY_CAPACITY = 64;

哈希表的大小必须要2次幂

在HashMap的构造方法中可以看到HashMap的初始容量必须要2次幂大小：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public HashMap(int initialCapacity, float loadFactor) {
  // 省略...
  this.loadFactor = loadFactor;
  this.threshold = tableSizeFor(initialCapacity);
}

static final int tableSizeFor(int cap) {
  int n = cap - 1;
  n |= n >>> 1;
  n |= n >>> 2;
  n |= n >>> 4;
  n |= n >>> 8;
  n |= n >>> 16;
  return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}

此处会把初始容量大小设置为最接近传入值的2次幂值，如构造参数传入3，这设置初始容量为4。

计算哈希表索引

在往哈希表中放置元素时，必然要先计算元素应该放在哪个位置：

1
2
3
4
5
6
7
8
9
10
11
12
public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    // 省略....
    // 此处数组索引值使用的是(n-1) & hash，n为数组大小
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    // 省略....
}

其中在调用putVal时重新计算了key的hashCode，而最终使用的索引计算方式为(n-1) & hash：

其中hash()代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * Computes key.hashCode() and spreads (XORs) higher bits of hash
 * to lower.  Because the table uses power-of-two masking, sets of
 * hashes that vary only in bits above the current mask will
 * always collide. (Among known examples are sets of Float keys
 * holding consecutive whole numbers in small tables.)  So we
 * apply a transform that spreads the impact of higher bits
 * downward. There is a tradeoff between speed, utility, and
 * quality of bit-spreading. Because many common sets of hashes
 * are already reasonably distributed (so don't benefit from
 * spreading), and because we use trees to handle large sets of
 * collisions in bins, we just XOR some shifted bits in the
 * cheapest possible way to reduce systematic lossage, as well as
 * to incorporate impact of the highest bits that would otherwise
 * never be used in index calculations because of table bounds.
 */
static final int hash(Object key) {
  int h;
  return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

此处为什么需要重新定义一个hash方法，而不用key的hashCode方法呢？通过方法注释可以看到，因为哈希表(即HashMap)的大小使用的是2次幂，作者认为很容易产生冲突（假设大小n=16，那么(n-1)转为2进制就是1111，对于int类型的hashCode而言，只用到了最低4位进行计算），因此作者在速度，实用性和位扩展的质量上做了中和，而且现在的hashCode已经是合理分布了，同时HashMap也使用了树结构来解决大规模Hash冲突的问题，因而取了一种比较简单的方案，即高16位不变，将低16位和高16位做了一个异或。

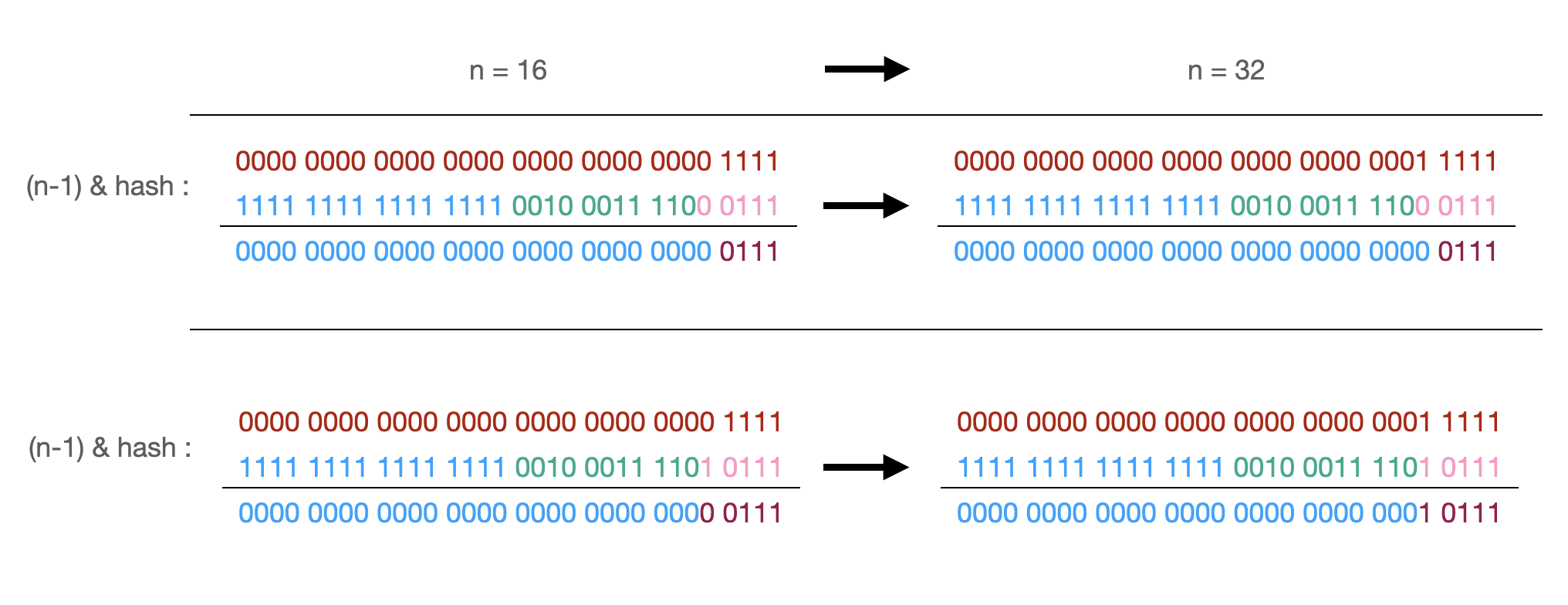
而数组中的索引使用的是(n-1) & hash，最终通过key计算数组索引就是下面这样：

map-hash

扩容

在哈希表的元素数量超过了扩容阈值时，哈希表会进行扩容，将大小扩大为原来的2倍：

1
2
3
4
5
6
7
8
9
10
11
12
/**
* Initializes or doubles table size.  If null, allocates in
* accord with initial capacity target held in field threshold.
* Otherwise, because we are using power-of-two expansion, the
* elements from each bin must either stay at same index, or move
* with a power of two offset in the new table.
*
* @return the table
*/
final Node<K,V>[] resize() {
   // .....
}

当初始化或者需要扩容时会调用resize()方法，扩容时会将容量变为原本大小的2倍，而且这样做会有个好处，因为容量大小使用的是2次幂，因此一旦触发了扩容操作，那么原本的key要不在原位置，要不只需要在偏移2次幂个位置(其实就是在原位置移动之前容量大小个位置)(在链表的情况下)，这样做的好处就是可以节省重新计算hash的时间：

map-resize